Radar Cross Section

This document records some possible useful rcs-related equations for my simulations 😄.

RCS Definition¹

The RCS represents an equivalent aperture surface area of the target, which captures a certain amount of incident radiation, and which, if re-radiated isotropically, would produce an equivalent scattered field at the receiver.

• For 2d target:

  $$\begin{array}{r}{\sigma }_{2d}=\{\begin{array}{l}\underset{\rho \to \mathrm{\infty }}{lim}\left[2\pi \rho \frac{S^s}{S^i}\right]\\ \underset{\rho \to \mathrm{\infty }}{lim}\left[2\pi \rho \frac{|E^s{|}^2}{|E^i{|}^2}\right]\\ \underset{\rho \to \mathrm{\infty }}{lim}\left[2\pi \rho \frac{|H^s{|}^2}{|H^i{|}^2}\right]\end{array}\end{array}.$$

• For 3d target:

  $$\begin{array}{r}{\sigma }_{3d}=\{\begin{array}{l}\underset{r\to \mathrm{\infty }}{lim}\left[4\pi r^2\frac{S^s}{S^i}\right]\\ \underset{r\to \mathrm{\infty }}{lim}\left[4\pi r^2\frac{|E^s{|}^2}{|E^i{|}^2}\right]\\ \underset{r\to \mathrm{\infty }}{lim}\left[4\pi r^2\frac{|H^s{|}^2}{|H^i{|}^2}\right]\end{array}\end{array}.$$

• Where $\rho ,r=$ distance from target to observation point.

  • $S^s,S^i=$ scattered, incident power density.
  • $E^s,E^i$ = scattered, incident electric fields.
  • $H^s,H^i=$ scattered, incident magnetic fields.

Monostatic and Bistatic RCS

Assuming a spherical coordinate system defined by $(\rho ,\theta ,\varphi )$, denote the incident wave direction as $({\theta }^i,{\varphi }^i)$ and scattered wave direction as $({\theta }_s,{\varphi }_s)$.

• RCS measured by ${\theta }_s={\theta }_i$ and ${\varphi }_s={\varphi }_i$ is called monostatic RCS (or backscattered RCS).
• RCS measured by ${\theta }_s\ne {\theta }_i$ and ${\varphi }_s\ne {\varphi }_i$ is called bistatic RCS.

Remark: In my opinion, monostatic RCS could be considered as a function of frequency and incident angles while bistatic RCS is more complex and can be considered as a function of frequency, incident angle, scattered angle, and bistatic angle.

Monostatic to Bistatic Equivalence²

Kell’s Monostatic-to-Bistatic Theorem³

$${\sigma }_{bistatic}(\theta =\beta ,f)={\sigma }_{monostaic}(\theta =\beta /2,f\sec (\beta /2)).$$

Crispin’s Monostatic-to-Bistatic Equivalence Theorem⁴:

$${\sigma }_{bistatic}(\theta =\beta ,f)={\sigma }_M(\theta =\beta /2,f).$$

Here, $\beta$ refers to bistatic angle and $f$ refers to frequency.

Bistatic RCS Estimation of an ellipsoid^{5 6}

Reference⁶ corrects some mistakes of reference⁵.

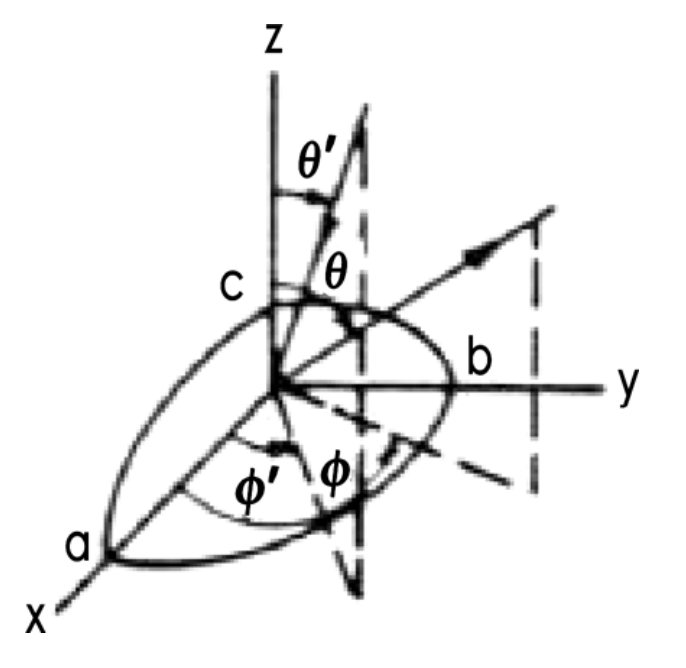
Considering an ellipsoid with its center at the origin:

$$\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1,$$

where, $a$,$b$,$c$ represent the length of the three semi-axes of the ellipsoid in the $x$, $y$, $z$ directions respectively.

Denote the incident and scattered wave directions in spherical coordinate form as $({\theta }_i,{\varphi }_i)$ and $({\theta }_s,{\varphi }_s)$ respectively. Here, ${\theta }_i,{\theta }_s$ refer to the incident and scattered aspect angles while ${\varphi }_i$, ${\varphi }_s$ refer to the incident and scattered azimuth angles of the ellipsoid relative to the transmitter and receiver.

• Then the bistatic RCS could be estimated by:

$${\sigma }_{bistatic}=\frac{4\pi a^2{b}^2{c}^2[(1+\cos {\theta }_i\cos {\theta }_s)\cos ({\varphi }_s-{\varphi }_i)+\sin {\theta }_i\sin {\theta }_s{]}^2}{{[a^2(\sin {\theta }_i\cos {\varphi }_i+\sin {\theta }_s\cos {\varphi }_s{)}^2+b^2(\sin {\theta }_i\sin {\varphi }_i+\sin {\theta }_s\sin {\varphi }_s{)}^2+c^2(\cos {\theta }_i+\cos {\theta }_s{)}^2]}^2}.$$

• For monostatic case (${\theta }_i={\theta }_s=\theta$, ${\varphi }_i={\varphi }_s=\varphi$), we have:

$${\sigma }_{monostatic}=\frac{\pi a^2{b}^2{c}^2}{[a^2{\sin }^2\theta {\cos }^2\varphi +b^2{\sin }^2\theta {\sin }^2\varphi +c^2{\cos }^2\theta {]}^2}.$$

• When $a=b=c=r$, we have rcs estimation of a sphere:

  $${\sigma }_{monostatic-sphere}=\pi r^2.$$

Radar Range Equation

• Bistatic radar range equation:

  $$P_r=\frac{P_t{G}_t{G}_r{\sigma }_B{\lambda }^2}{(4\pi {)}^3{R}_{Tx}^2{R}_{Rx}^2}.$$

• Monostatic radar range equation ($R_{Rx}=R_{Tx}=R$):

  $$P_r=\frac{P_t{G}_t{G}_r{\sigma }_M{\lambda }^2}{(4\pi {)}^3{R}^4}.$$

  Where:

  • $P_t$, $P_r$ refer to transmit and receive power.
  • $G_t$, $G_r$ refer to transmit and receive antenna gain.
  • ${\sigma }_B$ and ${\sigma }_M$ refer to bistatic and monostatic RCS.
  • $R_{Tx}$, $R_{Rx}$ refer to distance of transmitter-target and receiver-target.